上 代入法 連立 方程式 750587-連立 方程式 代入法 難問

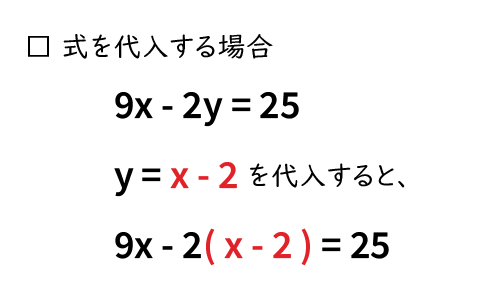
中学校2年生数学 連立方程式 代入法 成果主義 Itto個別指導学院 長野市の学習塾

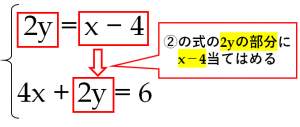
 國立台灣大學土木工程學研究所民國92年碩士學位論文摘要應用SCM於Timoshenko梁之分析研究研 究 生：楊耀昇指導教授：吳賴雲第一章 緒論對大多數工程技術問題，由於物體幾何形狀較複雜或問題的某些特徵非線性，故少有解析解。 一方の式を他方の式に代入することで1種類の文字を消去する ※ 多項式を代入する際はかっこが必要である。 (1)はかっこがなくても，代入した際の結果が同じとなるため書かれていない

連立 方程式 代入法 難問

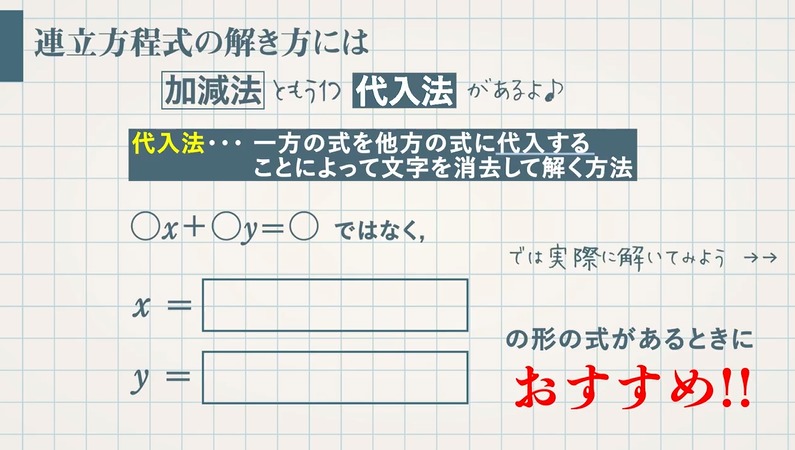
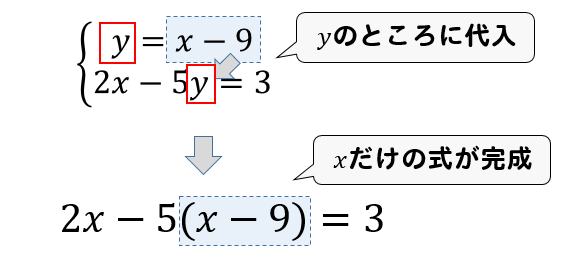
連立 方程式 代入法 難問-連立方程式とは2つの文字 (xとy)を含み、2つの式からなる方程式のこと。 連立方程式の解き方には 代入法 と 加減法 がある。 どちらの場合もxかyのどちらか 1つの文字を消去して解く 。 代入法 ≫ 加減法 片方の式が x = の形になっていれば、それを他方のxに代入することでxが消えてyだけの方程式ができる。 (y= の形ならyに代入する。 ) またx= やy= の形になっていなくても、式の変形によってx (ま連立一次方程式はさまざまな場面で登場し，特に応用的には重要な常微分方程式(第16, 18 章)， 偏微分方程式(第19 章) との関わりが深い。よって，行列の構造や問題，精度，コンピュータ環境 に適した多種多様な解法が提案されている。

次の連立方程式を代入法で解きなさい やり方を教えてください お願い致し Yahoo 知恵袋

計算方式は加減法・代入法を選択できます。 A=B=Cのような連立方程式を計算する場合は、電卓の①に入力し②は空欄で「計算」ボタンを押してください。 計算をやり直す場合は「クリア」ボタンを押すと電卓に入力された数値が削除されます。 連立方程連立方程式 練習問題 連立 代入法1 連立 代入法2 連立 加減法1 連立 加減法2 連立 加減法3 連立計算 分数1 連立計算 分数2 連立計算 分数3 連立計算 分数4 連立計算 小数1 連立計算 小数2 連立計算 小数3 かっこのある連立方程式 かっこのある連立方程式2 かっこのある連立方程式3 連立 (A=B=C) 連立 (A=B=C)2 連立 (A=B=C)3 連立 (A=B=C)4今回は連立方程式の解き方の一つである 代入法 について解説していきます。 代入法 は、 加減法 と同様に連立方程式を解く際に用いられる方法の1つです。 加減法でほとんどの問題を解くことが出来ますが、代入法を用いたほうがより早く、楽に解くこと

代わりに入れる 連立方程式の解き方は 2 2 種類です。 加減法と代入法です。 加減法はマスターしましたか？ 続いて、連立方程式の解き方の2代入法を学習しましょう。 例題1 次の連立方程式を代入法で解きなさい。 { 3x−y=2 y=x−4 { 3 x − y = 2 y = x − 4 解説 「代入」とは「代わりに入れる」ことです。 つまり、 y y の代わりに、それと等しい x−4 x − 4 でもいいじゃないか、ということです。 つ國立台灣大學土木工程學研究所民國92年碩士學位論文摘要應用SCM於Timoshenko梁之分析研究研 究 生：楊耀昇指導教授：吳賴雲第一章 緒論對大多數工程技術問題，由於物體幾何形狀較複雜或問題的某些特徵非線性，故少有解析解。解決此類問題常となり この連立方程式の答えは 代入法の手順としては となっている式にかっこをつける かっこをつけた式をもう一方の式に代入する あとは方程式を計算 至ってシンプル！ かっこをつけずに代入しちゃうと 符号ミスやかけ算忘れにつながるから

連立 方程式 代入法 難問のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン	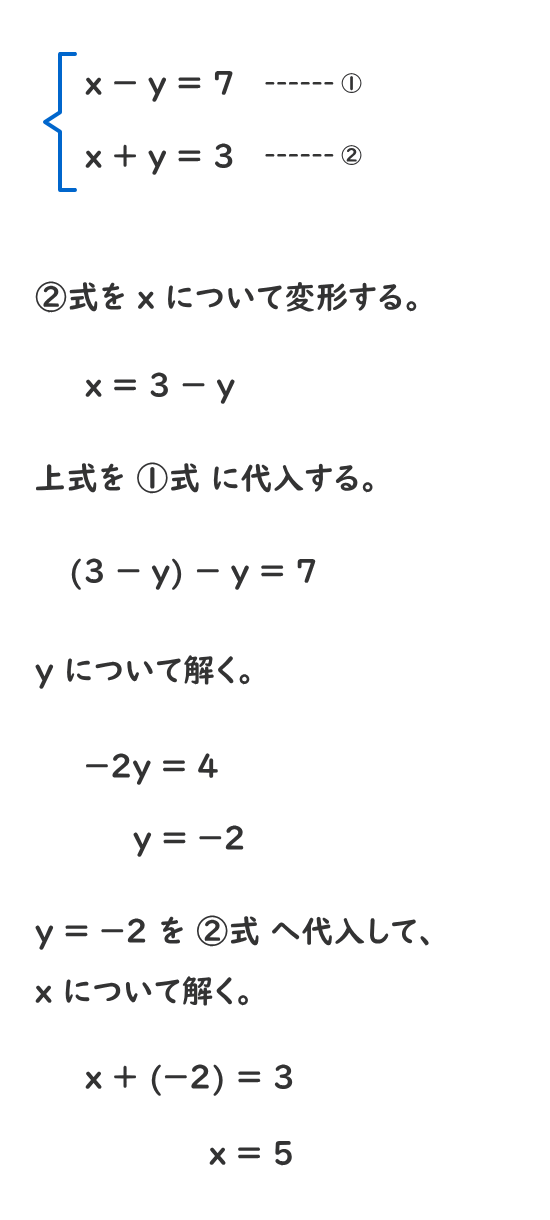連立方程式 代入法2 チーム エン
連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン	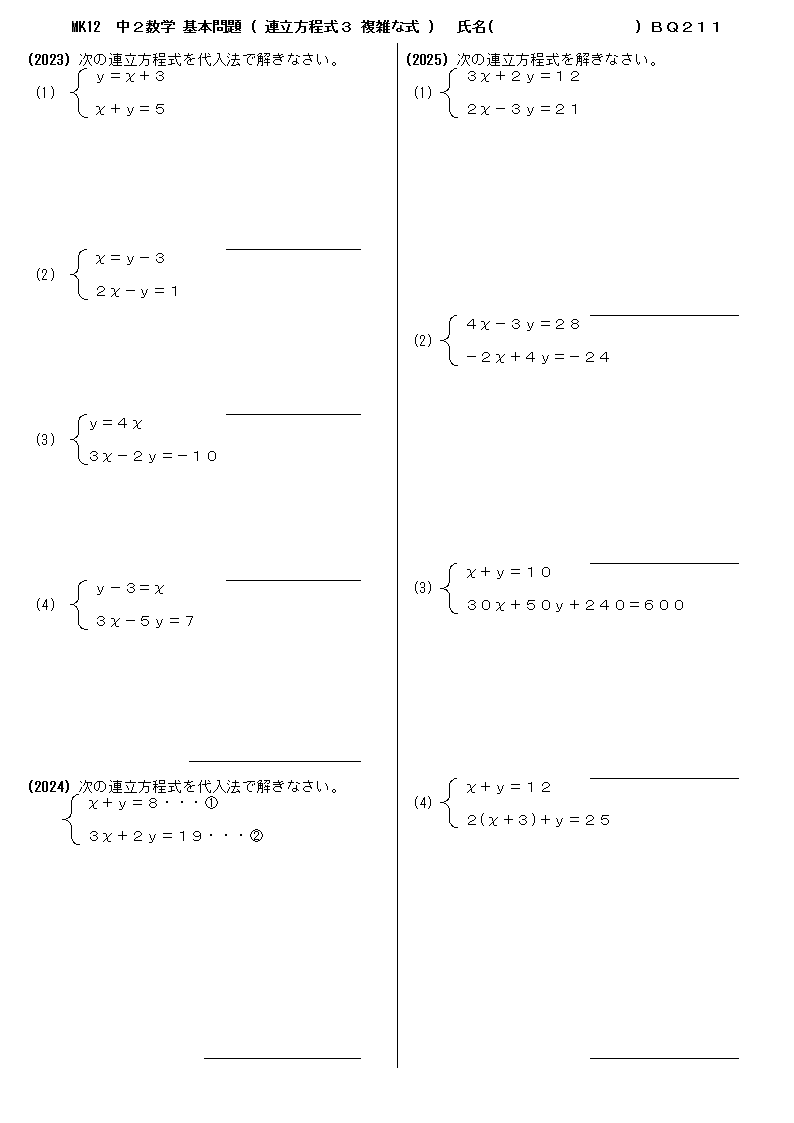連立方程式 代入法2 チーム エン
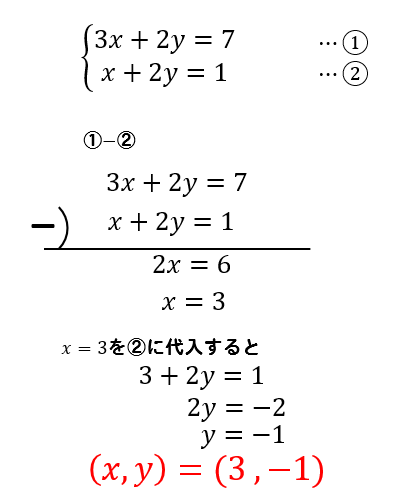連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン
連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン	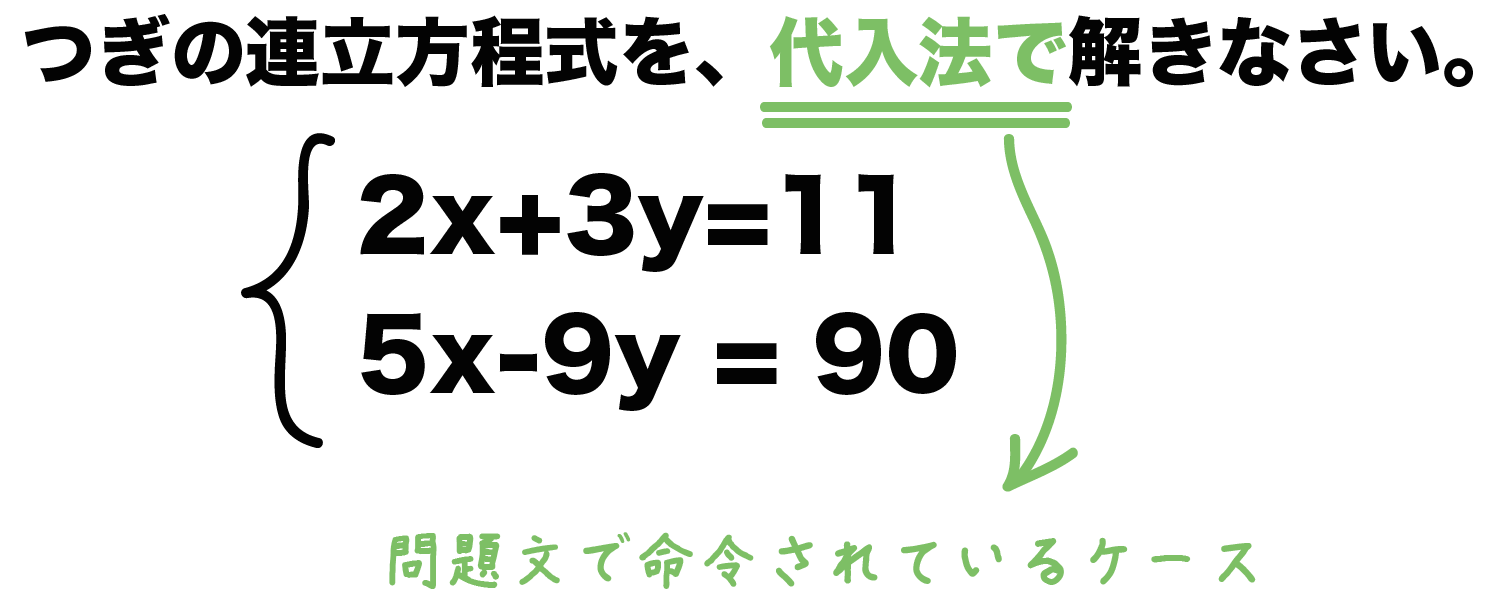連立方程式 代入法2 チーム エン
連立方程式 代入法2 チーム エン	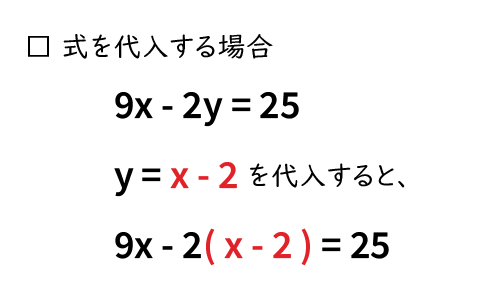連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン
連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン	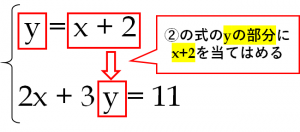連立方程式 代入法2 チーム エン
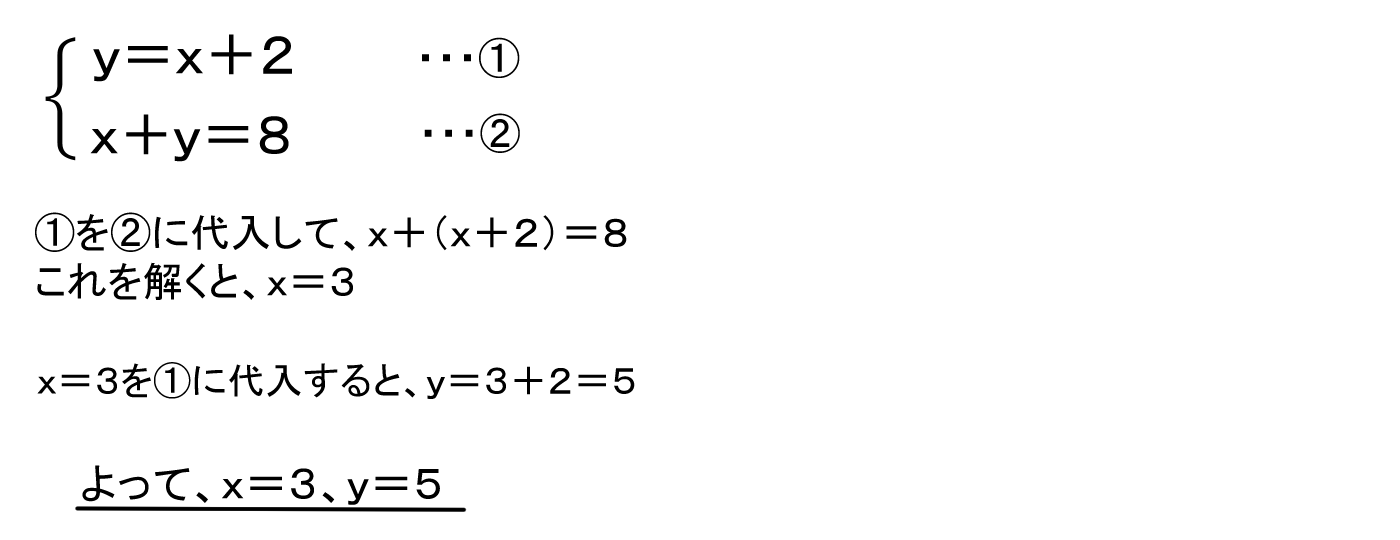連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン
連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン
連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン	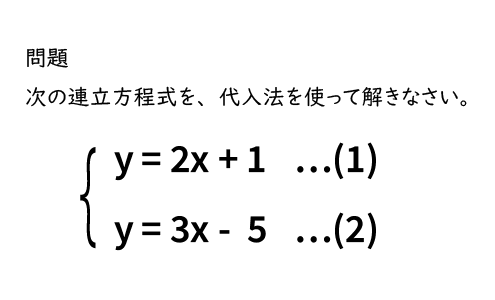連立方程式 代入法2 チーム エン
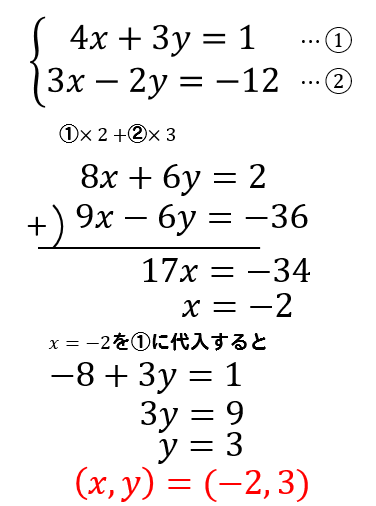連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン	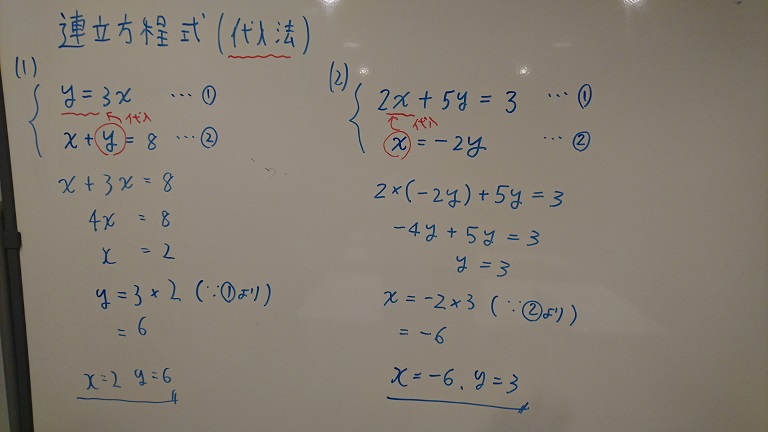連立方程式 代入法2 チーム エン
連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン	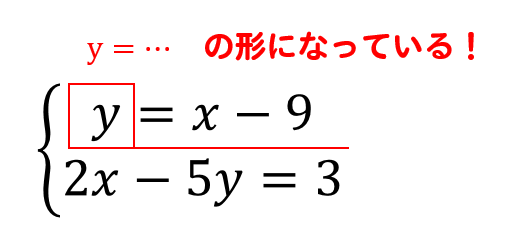連立方程式 代入法2 チーム エン
連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン
連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン
連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン
連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン
連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン
連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン
連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン
連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン
連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン
連立方程式 代入法2 チーム エン	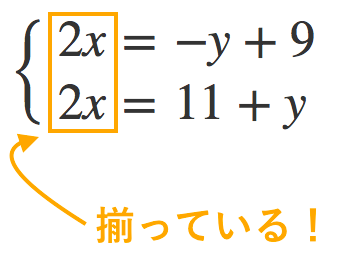連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン
連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン	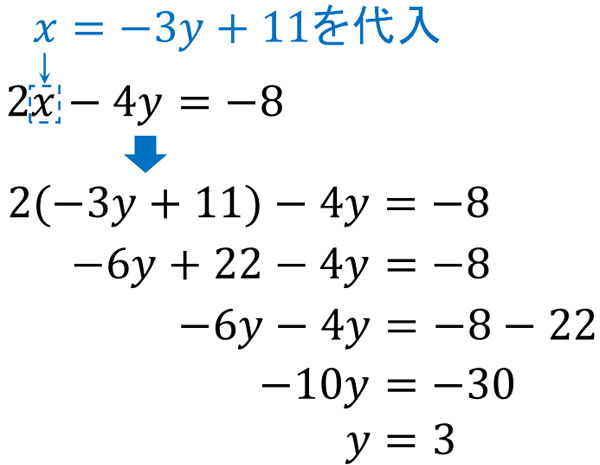連立方程式 代入法2 チーム エン
連立方程式 代入法2 チーム エン	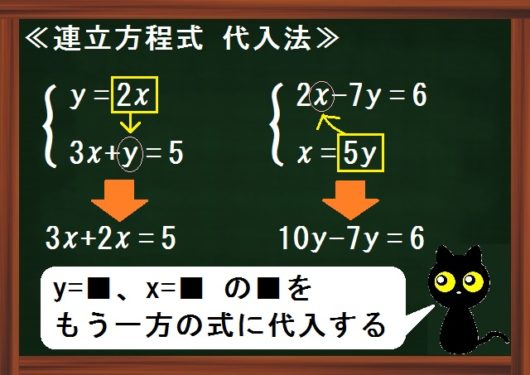連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン
連立方程式 代入法2 チーム エン	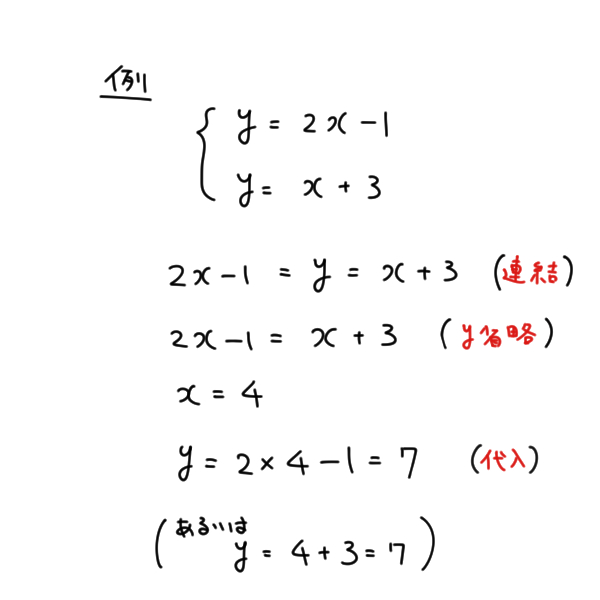連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン
連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン
連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン
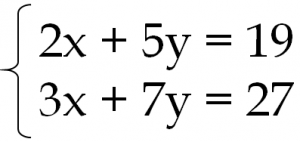連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン
連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン
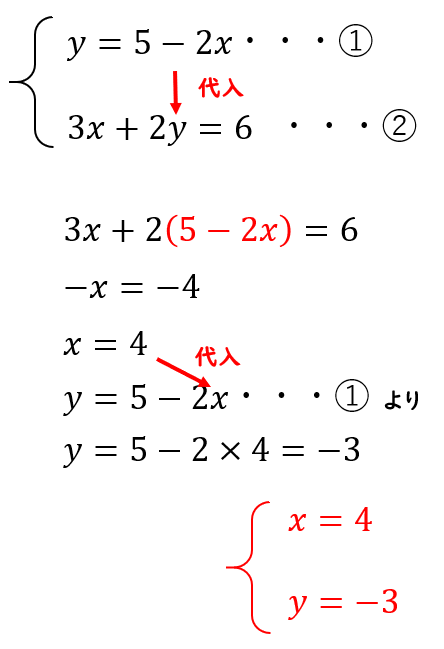連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン
連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン
連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン
連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン	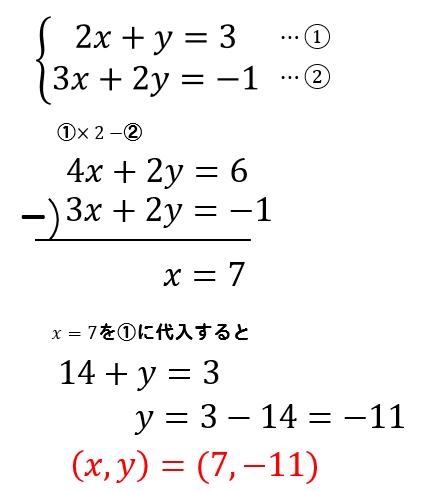連立方程式 代入法2 チーム エン
連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン
連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン
連立方程式 代入法2 チーム エン	連立方程式 代入法2 チーム エン

故 x＝3， y＝2 為二元聯立方程組的解。 三、解應用問題 ： 利用二元一次聯立方程式解決生活情境中的問題，解題步驟為： 1 認清題意設定兩個適當的未知數。 2 依題意列出二元一次聯立方程式。 3 利用代入消去法或加減消去法解二元一次聯立方程式。代入法とは、 「一方にもう一方の式を代入することで文字を一つ消去し、連立方程式を解く方法」 です。 たとえば以下の連立方程式を代入法で解いてみましょう。 {x＝2y x＝y 5 { x ＝ 2 y x ＝ y 5 このように一方の方程式が「 x＝ x ＝ 」や「 y＝ y ＝ 」の形なら、そのまま右辺をもう一方の式に代入することができます。 こうすることで一方の文字が消えるので、一次方程式になります。 一次方

Incoming Term: 連立 方程式 代入法 なぜ, 連立 方程式 代入法 難問, 連立 方程式 代入法,